Euler-bernoulli

In Onderstaande berekening wordt de Differentiaalvergelijking voor de "Euler-Bernoulli staaf" afgeleid. De belangrijkste aanname in deze theorie is dat vlakke doorsnede vlak blijven en loodrecht op de staafas, in een staaf belast op buiging. Deze aanname is geldig wanneer de vervorming door dwarskracht en torsie erg klein is ten opzichte van de vervorming door normaalkracht en buiging, slanke staven. Indien dit niet het geval is kan de Timoshenko staaf theorie worden toegepast.
Deze theorie geldt alleen voor elastische materialen die worden belast op buiging met kleine hoekverdraaiingen.

Aanname assenstelsel en positieve richting

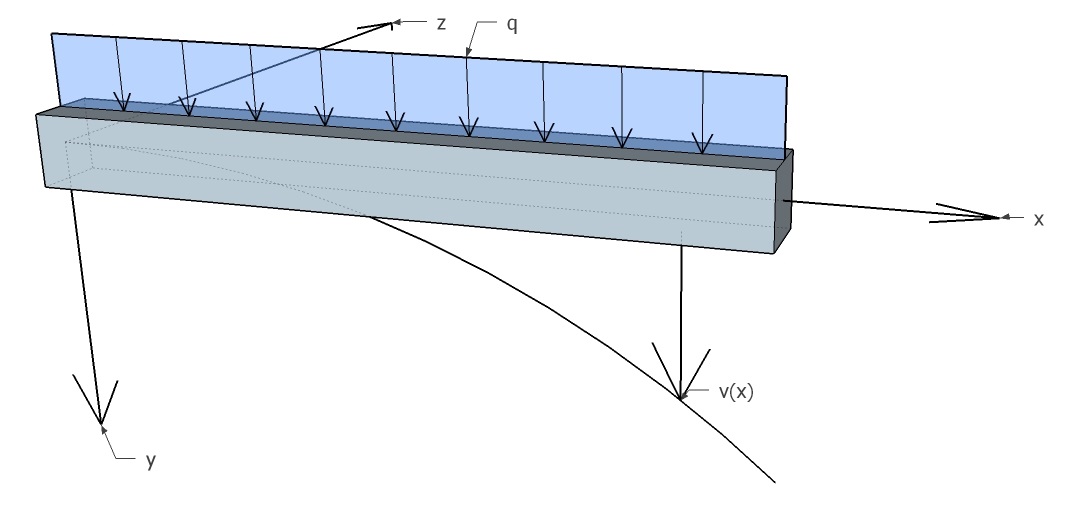
Voor de afleiding van de differentiaal vergelijking zal allereerst een assenstelsel en de positieve richtingen van de krachten moeten worden aangenomen. Wanneer er een ander assenstelsel wordt gebruikt zal de differentiaal vergelijking er anders uitzien.

Figuur 1 staaf belast op buiging

Zoals te zien in figuur 1 is de y as naar beneden aangenomen. Hier is voor gekozen omdat zakking en belasting naar beneden dan positief zijn. Voor constructieve berekeningen is dit een aanname waardoor de resultaten duidelijker worden.

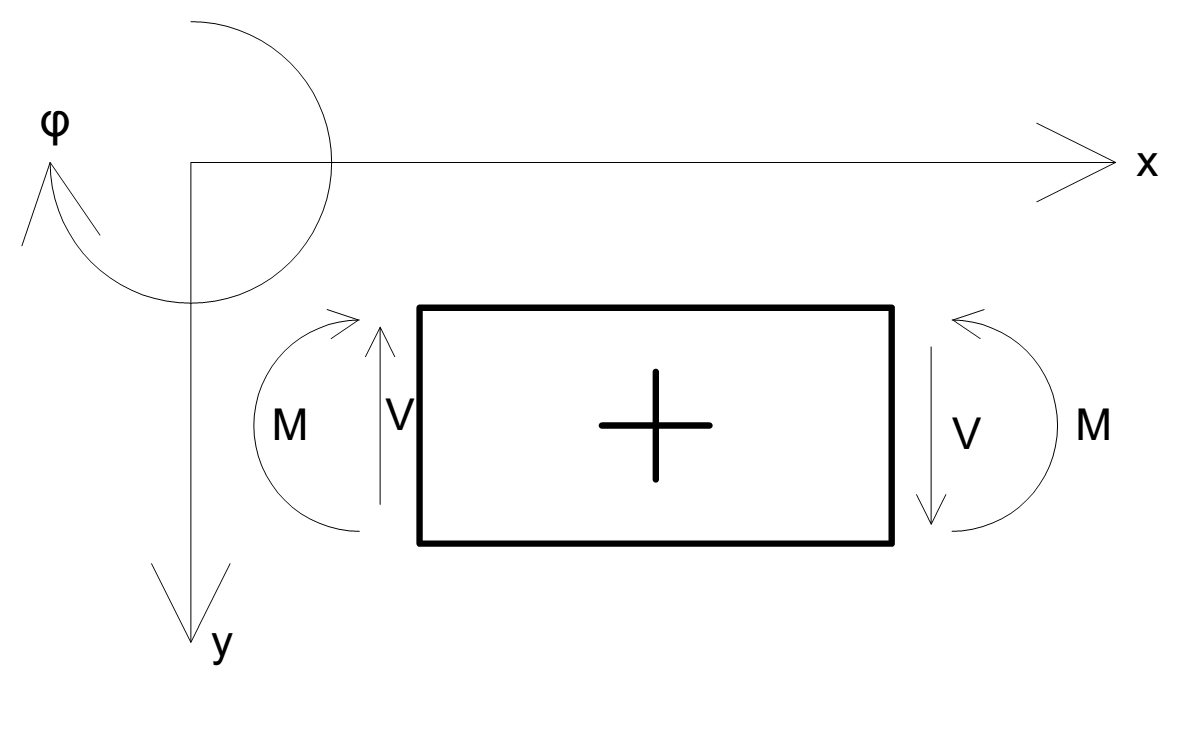Figuur 2 Vrij lichaamsdiagram met assenstelsel	Figuur 3 Buiging ten gevolge van een positief moment

In figuur 2 is het vrij lichaamsdiagram te zien met alle krachten in de positieve richting. In figuur 3 wordt de kromming ten gevolge van een positief moment weergegeven.

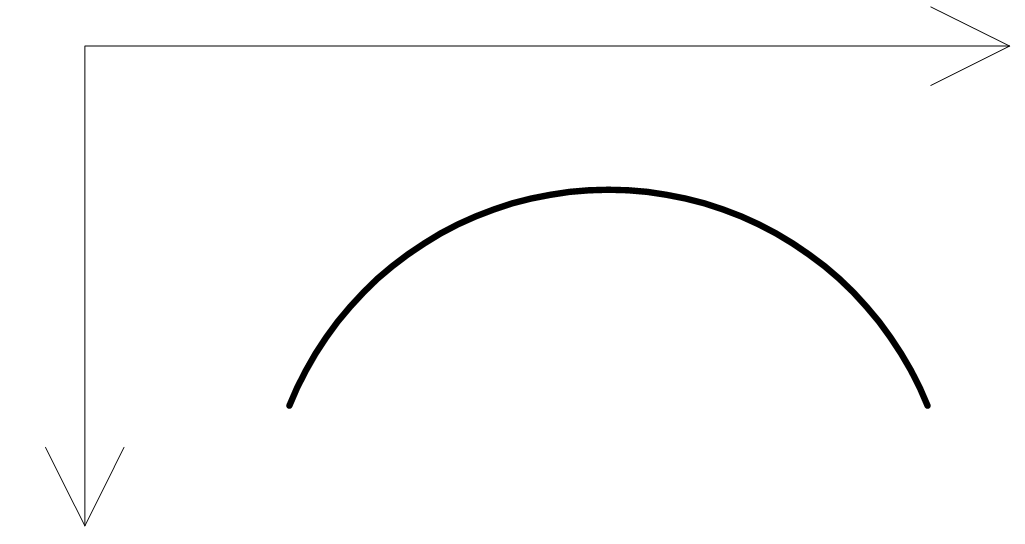Figuur 4 positieve kromming

In figuur 4 is de positieve kromming weergegeven in het bijhorend assenstelsel. Dit is de positieve kromming omdat: $\frac{{{d}^{2}}y}{d{{x}^{2}}}>0$. De kromming ten gevolgen van een positief moment is dus negatief.

Kinematische vergelijkingen

De kinematische relaties geven het verband tussen vervorming en verplaatsing.

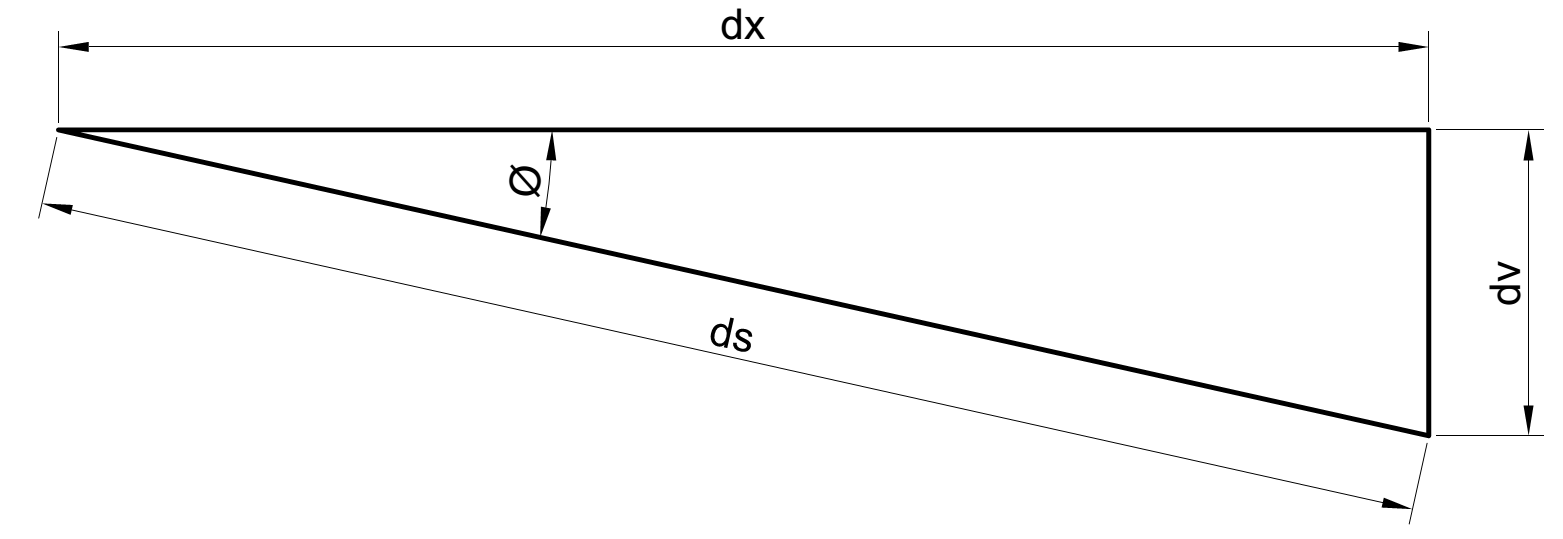Figuur 5 Geometrie	Figuur 6 Uitvergroting van figuur 5

In figuur 5 is de zakking van een staaf te zien waarin de afstand dx oneindig klein is. Op punt x is de zakking gelijk aan v en op punt x+dx is deze gelijk aan v+dv. Met eenvoudige geometrische analyse kunnen we stellen dat:

$ds=\rho \cdot d\theta \to \rho =\frac{ds}{d\theta }$ en $\kappa =\frac{1}{\rho }=\frac{d\theta }{ds}$

waarin ρ is de straal van de kromming en κ is de kromming.

De helling van de zakkingslijn is gelijk aan $\frac{dv }{dx}$ . In figuur 6 is te zien dat dit gerelateerd is aan de hoek van de rotatie:

$\tan \theta =\frac{dv}{dx}$

Omdat dx oneindig klein is kan er worden aangenomen dat ds recht is en geldt ook:

$\cos \theta =\frac{dx}{ds}$

De theorie gaat uit van kleine hoeken daarom kunnen we zeggen dat sinθ ≈ tanθ ≈ θ en cosθ ≈ 1. Daaruit volgt dat ds=dx en dus:

$\kappa =\frac{1}{\rho }=\frac{d\theta }{dx}$ en $\frac{dv}{dx}=\theta$

(1), (2)

Door vergelijking 1 en 2 samen te voegen krijgen we de volgende vergelijking:

$\frac{{{d}^{2}}v}{d{{x}^{2}}}=\kappa $

(3)

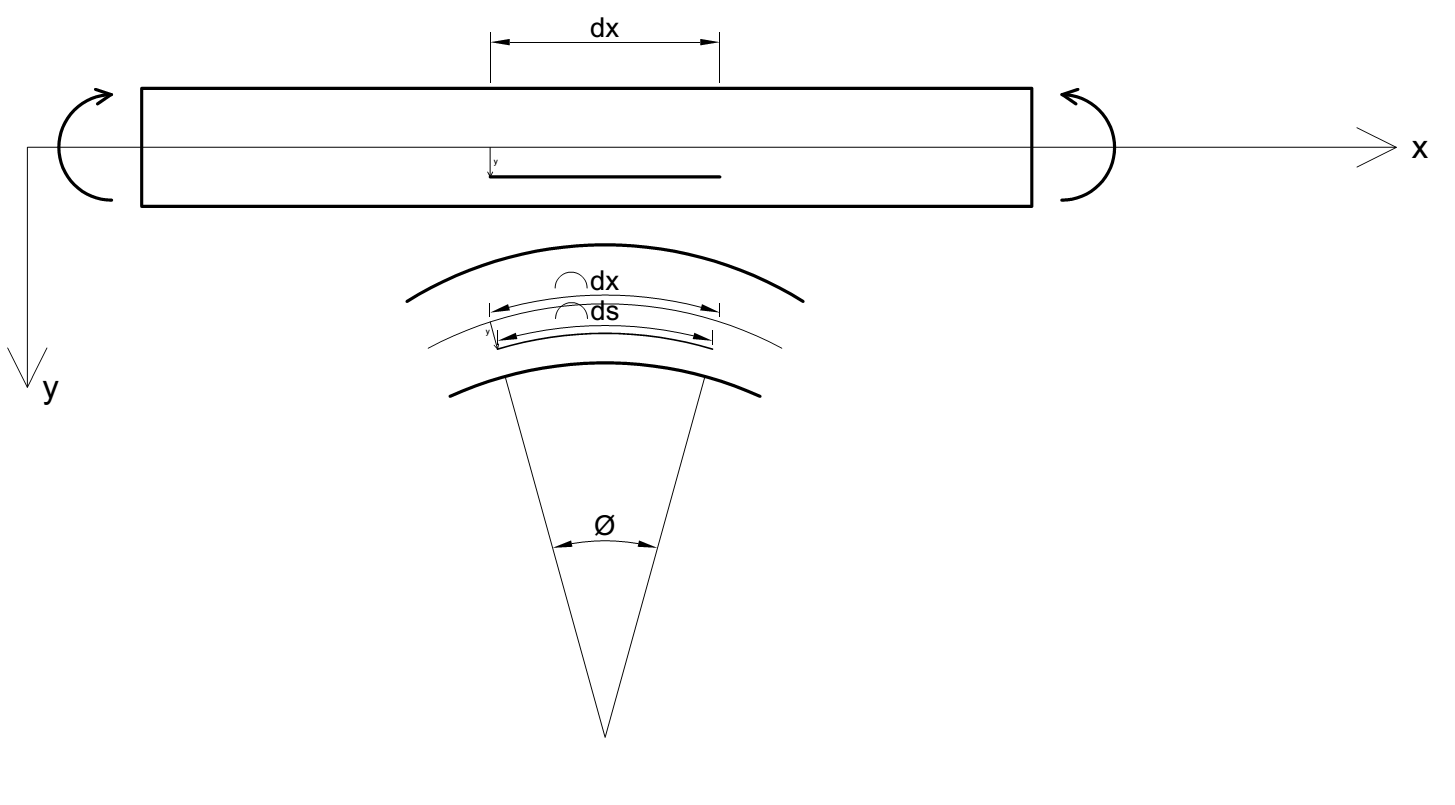Figuur 7 relatie kromming en rek

Om de relatie te vinden tussen de kromming en de bijbehorende vervorming bekijken we een gedeelte van een staaf in zuivere buiging door 2 momenten (zie figuur 7). De negatieve momenten veroorzaken een positieve kromming (volgens figuur 2 en 4). De vezels in de bovenkant verlengen en die in de onderkant verkorten. In de neutrale lijn veranderen deze niet in lengte. De lengte van dx=ρ*dθ.
Om de relatie te vinden beschouwen we de vezel op een afstand y vanaf de neutrale as. Deze vezel heeft na de buiging een lengte ds, ds=(ρ-y)dθ.De rek in deze vezel is gelijk aan ΔL/L, samen met vergelijking (1) volgt hieruit:

$\varepsilon =\frac{ds-dx}{dx}=\frac{(\rho -y)d\theta -\rho \cdot d\theta }{dx}=-y\frac{d\theta }{dx}=-y\kappa =-\frac{{{d}^{2}}v}{d{{x}^{2}}}y$

(4)

Evenwichtsvergelijkingen

De relatie tussen belasting, dwarskracht en momenten kan worden afgeleid door evenwicht in krachten in een oneindig klein element.

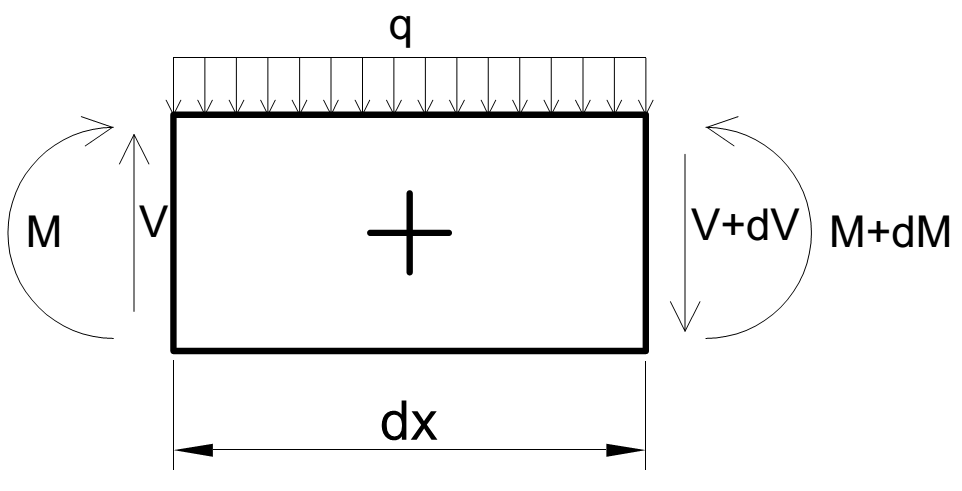Figuur 8 Evenwicht

De relatie tussen dwarskracht en verticale belasting kan worden verkregen door het evenwicht in verticale krachten: $\sum{{{F}_{v}}}=0$
$\sum{{{F}_{v}}}=-V+q\cdot dx+V+dV=0$

$q\cdot dx+dV=0\to \frac{dV}{dx}=-q$

(5)

De relatie tussen dwarskracht en moment kan worden verkregen door de som van de momenten. Deze som is gelijk aan 0. We nemen de som van de momenten om het middenpunt van het oneindig kleine element: $\sum{M}=0\to -M-V\cdot \frac{1}{2}dx-(V+dV)\cdot \frac{1}{2}dx+M+dM=0$

$-V\cdot dx+q\cdot \frac{1}{2}d{{x}^{2}}+dM=0$

dx is oneindig klein, dx² is daardoor verwaarloosbaar.

$-Vdx+dM=0\to \frac{dM}{dx}=V$

(6)

Constitutieve vergelijkingen

Volgens de wet van Hooke geldt dat σ=E*ε, dit samen met vergelijking 4 geeft: ${{\sigma }_{x}}=E\cdot {{\varepsilon }_{x}}=-E\cdot \kappa \cdot y$

Figuur 9 Moment

Figuur 9 geeft een deel van een staaf weer waar het moment aan de rechterkant is vervangen door de spanning. Om evenwicht te hebben in dit deel van de staaf moet gelden dat de som van σ*dA*y gelijk is aan het moment dus: $M=\int{\sigma \cdot y\cdot dA}$
Hieruit volgt met de uitdrukking van sigma: $M=\int{\sigma \cdot y\cdot dA}=-\int{E\cdot \kappa \cdot {{y}^{2}}\cdot dA}$ met $\int{{{y}^{2}}dA}=I$
Wanneer E en I gelijk blijven over de lengte volgt hieruit: $M=-\int{E\cdot \kappa \cdot {{y}^{2}}\cdot dA}=-EI\cdot \kappa$

Samen met uitdrukking (3) $M=-EI\frac{{{d}^{2}}v}{d{{x}^{2}}}$

(7)

Nu zijn alle vergelijkingen afgeleid en kunnen deze worden samengebracht, door vergelijking (5) en (6) te combineren krijgen we:

$\frac{{{d}^{2}}M}{d{{x}^{2}}}=-q$

Door deze vergelijking te combineren met (7) verkrijgen we:

$\frac{{{d}^{2}}}{d{{x}^{2}}}(-EI\frac{{{d}^{2}}M}{d{{x}^{2}}})=-q$

Als EI constant is over de lengte van de staaf kan deze uit de differentiaal vergelijking gehaald worden:

$EI\frac{{{d}^{4}}v}{d{{x}^{4}}}=q$