Normaalkracht Vervorming
In Onderstaande berekening wordt de Differentiaalvergelijking voor normaalkracht vervorming uitgewerkt. Dit is een van de eenvoudigste vervormings mechanisme. Toch kan er met behulp van deze differentiaal vergelijking veel constructieve probleme mee worden beschreven. Onderstaande afleiding geld alleen voor elastische materialen. Er wordt ook aangenomen dat de normaalkracht aangrijpt in het zwaartepunt van de doorsnede.
Aanname assenstelsel en positieve richting
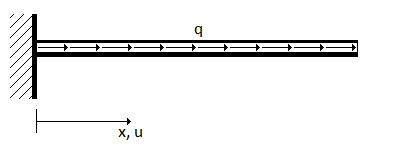 | 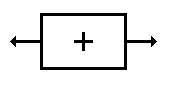 |
Figuur 1 | Figuur 2 |
Kinematische vergelijkingen
Kinematische betrekkingen beschrijven het verband tussen vervormingsgrootheden en verplaatsingsgrootheden
De staaf weergegeven in figuur 1 verlengt wordt verlengt. Op locatie x is de verlenging gelijk aan u(x), op locatie x+dx is de verlenging gelijk aan u(x+dx)=u+du met dx is oneindig klein.
$\varepsilon =\frac{u(x+dx)-u(x)}{dx}=\frac{u(x)+du-u(x)}{dx}=\frac{du}{dx}$ | (1) |
Constitutieve vergelijkingen
Constitutieve betrekkingen beschrijven de relatie tussen de kracht en vervorming.
De wet van Hooke beschrijft de relatie tussen de spanning en de rek in een vezel. $\sigma =E\cdot \varepsilon$ | (2) |
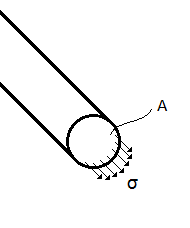 | 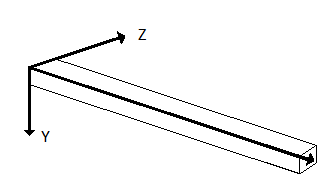 | 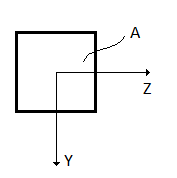 |
Figuur 3 | Figuur 4 | Figuur 5 |
Formule 1 en 2 invullen: $N=\int\limits_{A}^{{}}{E\frac{du}{dx}dA}$ met $dA=dzdy $ (zie fig. 4 en fig. 5)
$\frac{du}{dx}$niet afhankelijk van z of y dus $N=\frac{du}{dx}\int\limits_{A}^{{}}{EdA}$ Als E constant $N=EA\frac{du}{dx}$ | (3) |
Evenwichtsvergelijkingen
In een statische constructie is er een evenwicht in allen krachten.
 |
Figuur 6 |
In deze constructie bevinden zicht alleen krachten in de x richting in één lijn. De som van deze krachten moet gelijk zijn aan 0.
$\sum{{{F}_{x}}}=0\to -N+qdx+N+dN=0$
Uit deze formule valt N weg $qdx+dN=0\to -\frac{dN}{dx}=q$ | (4) |
formule 3 samenvoegen met 4: $-\frac{d}{dx}(EA\frac{du}{dx})=q$ en als E is constant $-EA\frac{{{d}^{2}}u}{d{{x}^{2}}}=q$